문제
https://www.acmicpc.net/problem/1446
| 입력값 | n: 지름길 정보 갯수 d: 최종 목적지 위치(노드) n개의 지름길 정보 |
| 출력값 | 시작(0)에서 부터 지름길을 활용하여 최종 목적지 d까지 걸리는 최단 거리 |
풀이 방법
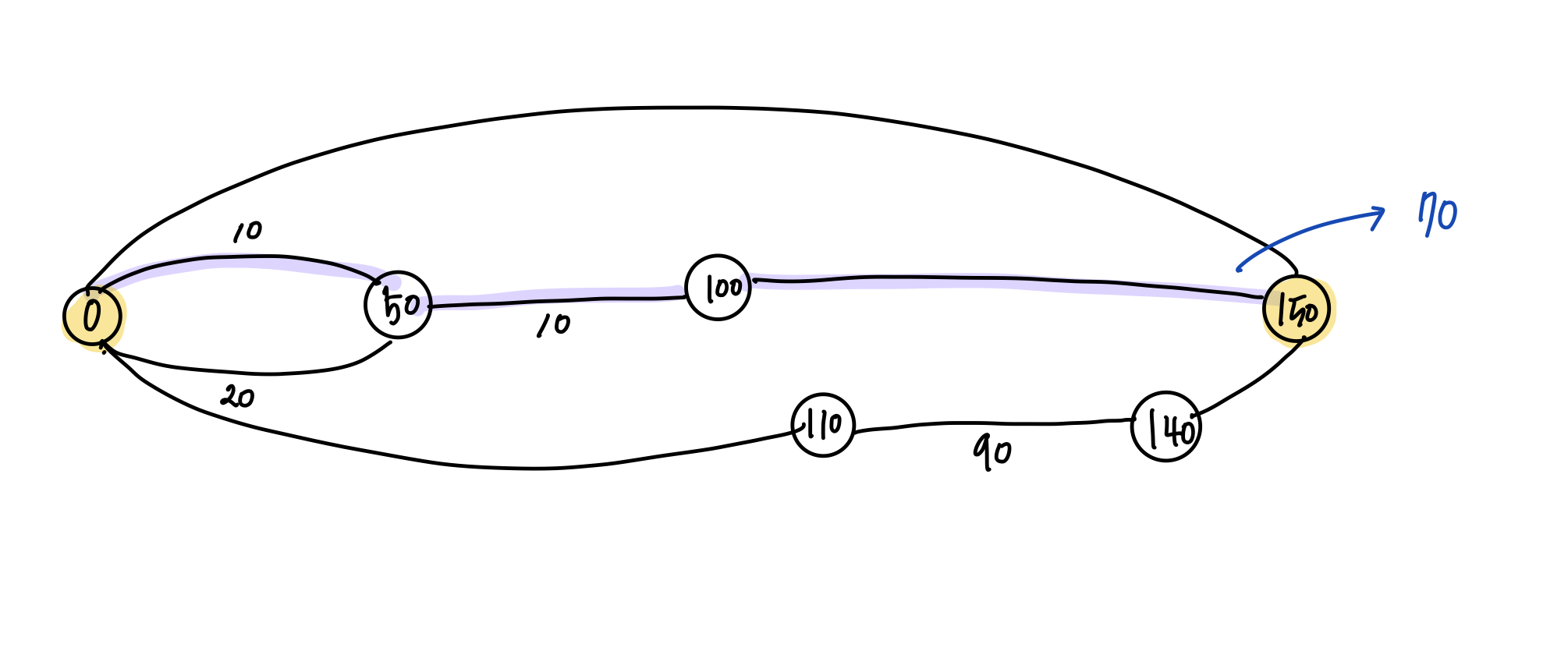
위 그림은 첫번째 예제를 그림으로 표현한 것이다.
시작 지점 0 에서 부터 도착 지점 150 까지의 거리는 150 - 0, 즉 150이다.
하지만 가는 길 마다 지름길로 연결된 각 노드들의 정보가 입력값으로 주어진다.
우리는 이 지름길을 활용하여 도착 지점 까지 갈 때, 거리의 최솟값을 구하고자 한다.
이 문제는 최단 거리 알고리즘 중 다익스트라를 사용하면 풀 수 있다.
각 위치별로 시작 시점에서 해당 노드까지의 최단 거리를 계속 갱신하면서 최종 도착 지점까지의 최단 거리를 구해보자.
사실 여기서 중요한 포인트는 0 ~ 150 까지, 총 151개의 노드가 있다는 점이다.
그래서 입력값에서 지름길 정보를 받을 때, 151개의 노드가 있다는 점을 참고하여 입력값을 저장해야 한다.
# 시작, 종료, 거리 정보가 든 배열 선언
# ------------ 1 ------------ #
short_road = [[] for _ in range(d+1)]
# ------------ 2 ------------ #
for i in range(d):
short_road[i].append([i+1, 1])
# ------------ 3 ------------ #
for i in range(n):
start, end, dist = map(int, input().split())
if end > d:
continue
short_road[start].append([end, dist])
위의 코드를 아래의 각 단계별 입력값의 데이터가 어떻게 저장되는지를 예시를 통해 설명하겠다.
지름길에 대한 정보를 입력 받기 전에 151(d+1) 개의 빈 리스트로 구성된 리스트를 선언하였다.
[[], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], []]
그리고 151개 노드들과 연결된 다음 노드와의 시작, 도착, 거리 정보를 업데이트 해주겠다.
즉, 아래 그림처럼 0번 노드는 사실 1번 노드와 거리 1로 연결되어 있고, 또 1번 노드는 2번 노드도 거리 1로 연결되어 있다.

이 내용을 반영하기 위해 2단계를 수행하였다.
[[[1, 1]], [[2, 1]], [[3, 1]], [[4, 1]], [[5, 1]], [[6, 1]], [[7, 1]], [[8, 1]], [[9, 1]], [[10, 1]], [[11, 1]], [[12, 1]], [[13, 1]], [[14, 1]], [[15, 1]], [[16, 1]], [[17, 1]], [[18, 1]], [[19, 1]], [[20, 1]], [[21, 1]], [[22, 1]], [[23, 1]], [[24, 1]], [[25, 1]], [[26, 1]], [[27, 1]], [[28, 1]], [[29, 1]], [[30, 1]], [[31, 1]], [[32, 1]], [[33, 1]], [[34, 1]], [[35, 1]], [[36, 1]], [[37, 1]], [[38, 1]], [[39, 1]], [[40, 1]], [[41, 1]], [[42, 1]], [[43, 1]], [[44, 1]], [[45, 1]], [[46, 1]], [[47, 1]], [[48, 1]], [[49, 1]], [[50, 1]], [[51, 1]], [[52, 1]], [[53, 1]], [[54, 1]], [[55, 1]], [[56, 1]], [[57, 1]], [[58, 1]], [[59, 1]], [[60, 1]], [[61, 1]], [[62, 1]], [[63, 1]], [[64, 1]], [[65, 1]], [[66, 1]], [[67, 1]], [[68, 1]], [[69, 1]], [[70, 1]], [[71, 1]], [[72, 1]], [[73, 1]], [[74, 1]], [[75, 1]], [[76, 1]], [[77, 1]], [[78, 1]], [[79, 1]], [[80, 1]], [[81, 1]], [[82, 1]], [[83, 1]], [[84, 1]], [[85, 1]], [[86, 1]], [[87, 1]], [[88, 1]], [[89, 1]], [[90, 1]], [[91, 1]], [[92, 1]], [[93, 1]], [[94, 1]], [[95, 1]], [[96, 1]], [[97, 1]], [[98, 1]], [[99, 1]], [[100, 1]], [[101, 1]], [[102, 1]], [[103, 1]], [[104, 1]], [[105, 1]], [[106, 1]], [[107, 1]], [[108, 1]], [[109, 1]], [[110, 1]], [[111, 1]], [[112, 1]], [[113, 1]], [[114, 1]], [[115, 1]], [[116, 1]], [[117, 1]], [[118, 1]], [[119, 1]], [[120, 1]], [[121, 1]], [[122, 1]], [[123, 1]], [[124, 1]], [[125, 1]], [[126, 1]], [[127, 1]], [[128, 1]], [[129, 1]], [[130, 1]], [[131, 1]], [[132, 1]], [[133, 1]], [[134, 1]], [[135, 1]], [[136, 1]], [[137, 1]], [[138, 1]], [[139, 1]], [[140, 1]], [[141, 1]], [[142, 1]], [[143, 1]], [[144, 1]], [[145, 1]], [[146, 1]], [[147, 1]], [[148, 1]], [[149, 1]], [[150, 1]], []]
이렇게 초기 작업을 해준 다음에 해당 리스트로 지름길 정보를 업데이트 한다.
[[[1, 1], [50, 10], [50, 20]], [[2, 1]], [[3, 1]], [[4, 1]], [[5, 1]], [[6, 1]], [[7, 1]], [[8, 1]], [[9, 1]], [[10, 1]], [[11, 1]], [[12, 1]], [[13, 1]], [[14, 1]], [[15, 1]], [[16, 1]], [[17, 1]], [[18, 1]], [[19, 1]], [[20, 1]], [[21, 1]], [[22, 1]], [[23, 1]], [[24, 1]], [[25, 1]], [[26, 1]], [[27, 1]], [[28, 1]], [[29, 1]], [[30, 1]], [[31, 1]], [[32, 1]], [[33, 1]], [[34, 1]], [[35, 1]], [[36, 1]], [[37, 1]], [[38, 1]], [[39, 1]], [[40, 1]], [[41, 1]], [[42, 1]], [[43, 1]], [[44, 1]], [[45, 1]], [[46, 1]], [[47, 1]], [[48, 1]], [[49, 1]], [[50, 1]], [[51, 1], [100, 10]], [[52, 1]], [[53, 1]], [[54, 1]], [[55, 1]], [[56, 1]], [[57, 1]], [[58, 1]], [[59, 1]], [[60, 1]], [[61, 1]], [[62, 1]], [[63, 1]], [[64, 1]], [[65, 1]], [[66, 1]], [[67, 1]], [[68, 1]], [[69, 1]], [[70, 1]], [[71, 1]], [[72, 1]], [[73, 1]], [[74, 1]], [[75, 1]], [[76, 1]], [[77, 1]], [[78, 1]], [[79, 1]], [[80, 1]], [[81, 1]], [[82, 1]], [[83, 1]], [[84, 1]], [[85, 1]], [[86, 1]], [[87, 1]], [[88, 1]], [[89, 1]], [[90, 1]], [[91, 1]], [[92, 1]], [[93, 1]], [[94, 1]], [[95, 1]], [[96, 1]], [[97, 1]], [[98, 1]], [[99, 1]], [[100, 1]], [[101, 1]], [[102, 1]], [[103, 1]], [[104, 1]], [[105, 1]], [[106, 1]], [[107, 1]], [[108, 1]], [[109, 1]], [[110, 1]], [[111, 1], [140, 90]], [[112, 1]], [[113, 1]], [[114, 1]], [[115, 1]], [[116, 1]], [[117, 1]], [[118, 1]], [[119, 1]], [[120, 1]], [[121, 1]], [[122, 1]], [[123, 1]], [[124, 1]], [[125, 1]], [[126, 1]], [[127, 1]], [[128, 1]], [[129, 1]], [[130, 1]], [[131, 1]], [[132, 1]], [[133, 1]], [[134, 1]], [[135, 1]], [[136, 1]], [[137, 1]], [[138, 1]], [[139, 1]], [[140, 1]], [[141, 1]], [[142, 1]], [[143, 1]], [[144, 1]], [[145, 1]], [[146, 1]], [[147, 1]], [[148, 1]], [[149, 1]], [[150, 1]], []]
[[1, 1], [50, 10], [50, 20]]: 0번 노드와 원래부터 연결된 1번 노드와 지름길 정보 ((50, 10), (50, 20))를 저장한다.
[[51, 1], [100, 10]] : 50번 노드와 원래부터 연결된 51번 노드와 지름길 정보(100, 10)를 저장한다.
시작 노드 0과 연결된 1, 50 번 노드에 대한 최단 거리를 구한다.
이후에는 1, 50을 다음에 방문할 노드로 저장하여 각각 연결된 노드들과의 최단 거리를 업데이트 한다.
계속해서 연결된 노드를 확인하며 최단 거리를 구한다.
그리하면 최종적으로 도착 지점까지의 최단 거리를 업데이트 하여 값을 구할 수 있다.
작성 답안
import heapq
n, d = map(int, input().split())
# 시작, 종료, 거리 정보가 든 배열 선언
short_road = [[] for _ in range(d+1)]
print(short_road)
for i in range(d):
short_road[i].append([i+1, 1])
print(short_road)
for i in range(n):
start, end, dist = map(int, input().split())
if end > d:
continue
short_road[start].append([end, dist])
print(short_road)
# 시작(0) 부터 각 i 위치까지의 최단 거리는 큰값으로 저장
distance = [1000000 for i in range(d + 1)]
queue = []
# 시작노드, 비용
heapq.heappush(queue, (0, 0))
# distance[start] = 0
while queue:
# dist: 시작 - 현재 노드 까지의 최단 거리
dist, start = heapq.heappop(queue)
if dist > distance[start]:
continue
for i in short_road[start]:
cost = dist + i[1]
end = i[0]
if distance[end] > cost:
distance[end] = cost
# distance[d] = distance[end] + (d - end)
heapq.heappush(queue, (cost, end))
print(distance[d])
'코딩테스트' 카테고리의 다른 글
| [백준] 실버 4/Java - 2003 수들의 합 2 (0) | 2024.09.03 |
|---|---|
| [백준] 실버1/파이썬 - 11726 트리의 부모 찾기 (0) | 2024.08.12 |
| [Letecode/SQL] Number of Unique Subjects Taught by Each Teacher (no. 2356) (0) | 2024.04.15 |
| [Programmers] 코딩테스트 입문 - 잘라서 배열로 저장하기 (0) | 2023.11.16 |
| [Programmers] 코딩테스트 입문 - 양꼬치 (0) | 2023.11.15 |